There are things that I find personally significant. And there are things I share with many others. These two lists rarely intersect. Except for names.

I can't think of anything as personal, yet shared with so many people, as my name.

For this reason, I have always found baby names interesting. (I know I am not alone. There are 1.7B Google search results for "baby names".) In this post, I want to look at some trends in baby names as well as how the economy might be affecting what we name ourselves.

1. Data & Research Questions

Data

The Social Security Administration tracks names and their frequencies, going back to 1880. For my analysis, I used data from 1880 to 2018. These yearly datasets include the names of every American with a social security card (!!), except for names with less than 5 nameholders.

Research Questions

How have features of names (i.e: vowels, length, syllables) changed over time?
Are baby names becoming more or less unique?
How does the economy interact with naming trends? In particular, do names get more or less unique during periods of slow economic growth?

2. How Names Have Changed

Length and vowels

Names started out simple in the late 1800s.

They were short and had few vowels.

Then, from about 1900 to 1920, names began getting more complex. Vowel count and length increased. After the 1920s, as we entered the depression, name complexity declined. Complexity bottomed out in the 1950s. After that point, name complexity shot up, peaking in the end of the millennium.

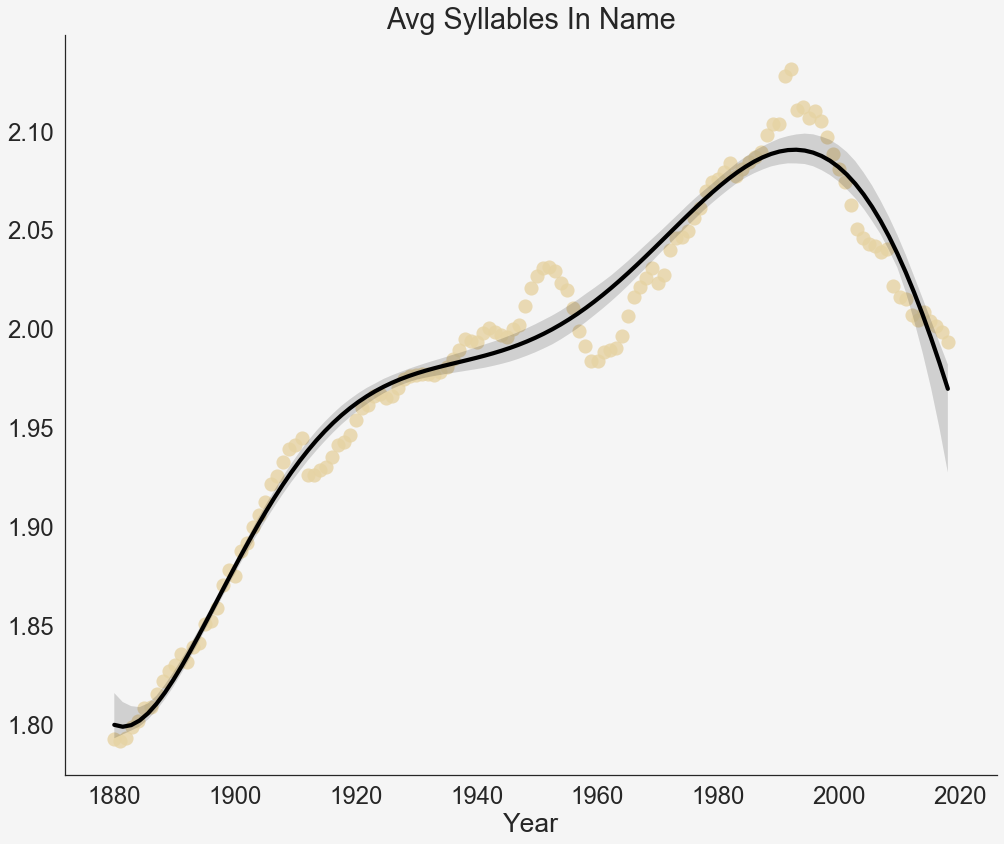
All this time, throughout the 20th century, the syllables in our names were steadily increasing.

Then after 2000, everything dropped. For the first time, we were using less syllables in our names. Names became shorter and less vowel-y, too. Our names are about as short as they were in the 1950s.

3. Uniqueness

The above highlights how the kinds of names have changed. But have names been getting more or less unique? To me, this is a good proxy of cultural "conformity".

Uniqueness Metrics

There are several ways we can think about name-uniqueness. And because this is a data science blog, I want to quickly discuss how each was calculated.

I measured the following at a yearly level.

Method 1: Probability 2 Random People Have The Same name

Suppose everywhere people go, they meet a stranger who has their name. In this world, names are not unique.

Formalizing this idea, I created a measure to calculate the probability 2 random Americans have the same name in a given year. So how is this calculated?

Let's just pick one name, "Josh". The probability of the first person having this name would be [Total Josh's / Total People]. At this point, we have removed one Josh from the population. Then the probability of the second person being named Josh is [Total Josh's -1 / Total People - 1]. This means the probability of both events occurring is ([Total Josh's / Total People]) * [Total Josh's -1 / Total People - 1].

Then, to compute the probability that 2 random Americans share ANY name, we would compute this formula for each name, and add the probabilities together.

If the probability of 2 people having the same name is low, then we can say names are unique.

method 2: Top 'N'

Suppose you walk into a room and everyone is named Michael or Sarah. If a high proportion of people have a "common" name, then names are not unique.

This measure simply looks at the proportion of people who have a name in the top n names. If many people in a given year have names in the top 10 (for example), then we can say names are NOT "unique".

method 3: Entropy

A third measure comes from information theory.

Shannon's entropy is an information-theoretic measure that can be thought to approximate the amount of 'surprise' in a distribution.

A probability space where every event is equally likely is extremely high-entropy. You really never know what will come next.

A probablity space where the probability of event A is 1, and the probability of every other event is 0, is extremely low-entropy. You won't be surprised.

If entropy of names is high in a given year, then we can say names are "unique".

uniqueness over time

Names were non-unique in the late 1800s. In 1880, 25% of Americans had a name in the ten most common names. And the chance of sharing a name with a random American was 1%.

As the century came to a close, uniqueness increased. By 1900, the odds of sharing the same name as a fellow American dropped to half a percent. And only 14% of Americans had a name in the top 10. Entropy increased, too.

For the next half of the 20th century, the trend reversed. We started becoming more conformist. Entropy of names dropped. The odds of sharing the same name as a stranger increased, and more Americans had a name in the top 10. By 1947, almost 20% of Americans had a name in the top 10. The period from 1930 to 1950 was peak name conformity.

Then after the 50s, uniqueness increased by all 3 measures. And names have been increasing in uniqueness ever since.

From 1880 to 2018, the odds of 2 random Americans sharing the same name went from 1% to a tenth of 1%; The share of Americans who have a name in the top 10 declined from 25% to 4%.

uniqueness and complexity

If vowels and length represent complexity, then a natural question to ask is: As names become more unique are they becoming more or less complex? Our complexity charts showed names became more complex since the 1960s. And our uniqueness charts showed names became more unique roughly during this period.

As the odds of 2 Americans sharing a name decrease, vowels as a proportion of a name increase (r=-0.42). This has been true since the 1880s. And after about 1930, there has been an inverse relationship between name length and the probability of sharing a name (r=-0.67).

It looks like as names become more unique, they also become more complex.

4. economics of a name

It certainly seems like we have become more individualistic, at least when it comes to names.

Does this hold during slow growth?

Perhaps names become less unique during periods of slow economic growth. If it's hard to get a job, then having the name "Unnamed Column" won't be too helpful. On the other hand, a bad economy might signal that the status quo does not work -- and this is reflected in unique names.

I found that the following uniqueness variables are lower during economic contractions (defined as negative GDP growth) than growth periods.

Share of Americans with name in top 10 most common names (t=2.3, p=0.03)
Share of Americans with name in top 20 most common names (t=2.3, p=0.03)
Share of Americans with name in top 50 most common names (t=2.1, p=0.04)
Probability 2 Americans share the same name (t= 2.4, p=0.03)

5. Conclusions

Complexity

Name complexity is camel-shaped. There are two humps--one at around 1920, and a higher one around 2000. Interestingly, both periods preceded recessions.

Uniqueness

Uniqueness decreased in the mid 20th century, but then increased after around 1960. Name uniqueness has been increasing ever since. From 1880 to 2018, the odds of 2 random Americans sharing the same name went from 1% to a tenth of 1%.

Economics & Names

During economic contractions, American names become (slighly) less unique;there is more conformity. The percentage of Americans having a name in the 10 most common names is about 3% larger in contraction periods as opposed to growth periods.

baby names and culture