Mathematical Art — Joshua Ashkinaze

Click a large image to see the full collection

what is ‘mathematical art’

Well, it really is ‘generative art’ but since AI-generated art I thought it simpler to call it mathematical art. Before AI-generated art, generative art described code to create compositions that have some built-in randomness. While AI art has some controversies, generative art is different. It is not trained on any prior data; it is written using your own algorithms (e.g: specifying shapes, colors, etc) to directly produce visuals. In my case, I like to combine color theory and statistical distributions to play with randomness in cool or aesthetically pleasing ways.

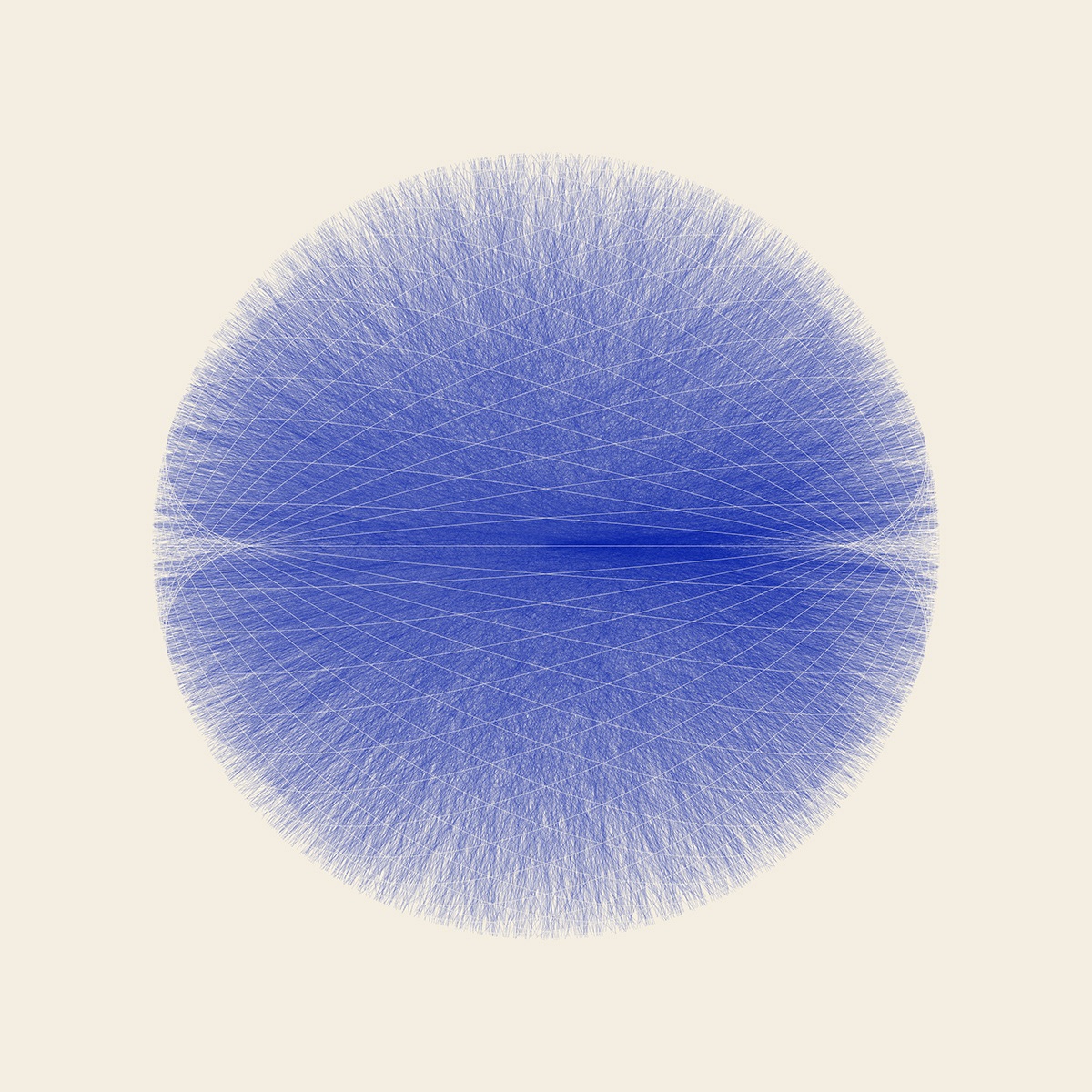
Dandelion Minds

There is a visual similarity between fluffy dandelion heads and the root-like synapses that run through our brains. A Dandelion Mind has the softness of the former and complexity of the latter.

Each Dandelion Mind starts with a circle with 3,000 Bezier curves etched inside of it. This circle is then rotated around the X and Y axes to create spherical shapes. Different rotation functions give different images.

Error Art: Grids of Accidental Ink Blots

Conventional calligraphy explores the perfectionist dimension of human handwriting. But what about the error-ridden aspect? I tried to generate what would happen if you removed everything but the accidental pen marks from a document. There's a chaotic art to ink blot errors that people with good handwriting miss. And (un)fortunately, I have very bad handwriting.

To simulate ink blot errors, I had to look at my own errors. I found that my penmanship errors look like either: elliptical ink blots, jagged lines, or accidental curves between letters. Using Processing, I generated random variations of these shapes joined together to simulate handwriting errors.

Disputed rainbows

These works are inspired by rainbows on partly overcast days.

Attractors

Each of these sketches is based on the Lorenz system of equations, which represent chaotic systems: If you start at particular values, you'll always get the same result. But change these starting values slightly and you'll get a vastly different result.

Sparse views

Something like 'sparsity' seems to come up a lot in art. Take glitch art and European impressionism. A common glitch art technique is the removal of contents from a scene via (say) black bars over an image. This is sparsity as removal of content. And in impressionism, images often look kind of blurred due to the "impasto" technique. This is sparsity as a lack of detail.

So here's my spin on sparsity. It's a glitchy, impressionistic approach.

Iterating up and down an image, I stamp a canvas with an image's color and then 'scribble' this color to nearby points. ('Scribbles' are made by (1) interpolating between short horizontal lines, (2) adding horizontal and vertical noise to each interpolated point, and (3) then joining these points together with curves). Visually, this extends an image's color - creating a blurred, impasto-like effect. The vertical distance between scribble rows is always larger than the height of scribbles. This creates gaps in the final image. Together, the scribbles and black space lead to a glitchy, impressionistic sparsity.

Tiled tides

I have always liked ripples, and wanted to experiment with designing my own. Each object is composed of a carpet of tiles. Each tile is a series of curves nested inside of one another. Tiles ripple out of the canvas according to various tide functions, and the closer to the viewer, the lighter the tile. Each of the 5 tide variations is presented at 3 levels of intensity.

Infinite Lawns

I had a feeling I was being architecturally trolled while entering a museum in Arizona.

The manicured walkway was so, excessively long. In our world of resource scarcity and climate change, big lawns aren't usually celebrated. But it got me thinking. In an alternative universe of unlimited resources, wouldn't it be interesting to have an infinite lawn? Here are some proposals.

Each lawn is drawn on a 3D canvas rotated on the x-axis by 45 degrees. This gives the illusion of infinite length. Each lawn's aesthetic can be described as 'LSD-Minimalist': Clean, modern, with a touch of hypnosis. Mathematically, each lawn is a grid of circles, with each circle's x-coordinate offset according to a different bivariate trig function.

If Circuits Wove

I tried to imagine what it would look like if circuits wove things. Each quilt is made of rectangular "patches" and recursively generated stitches alternating at multiples of 90 degrees. Sizes are drawn from the Pareto distribution.